publications
Thesis
2023
- Quantum Theory in Knowledge Representation: A Novel Approach to Reasoning with a Quantum Model of ConceptsWard Gauderis and Geraint WigginsVrije Universiteit Brussel, Aug 2023
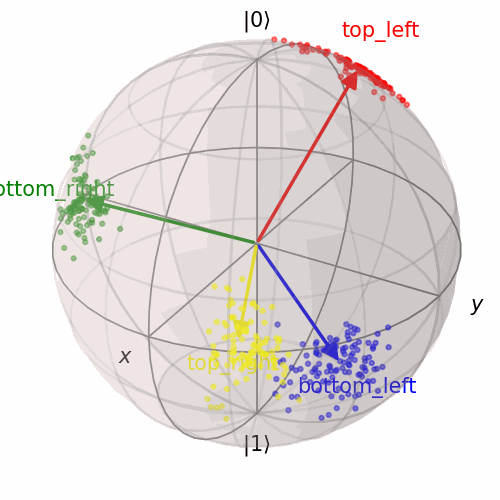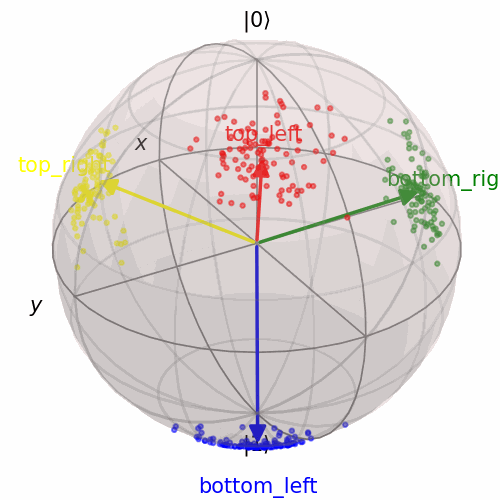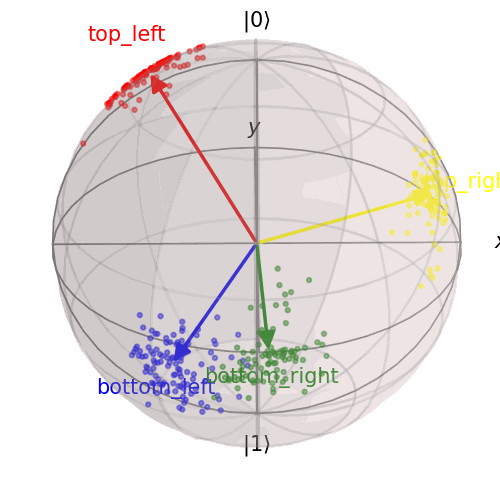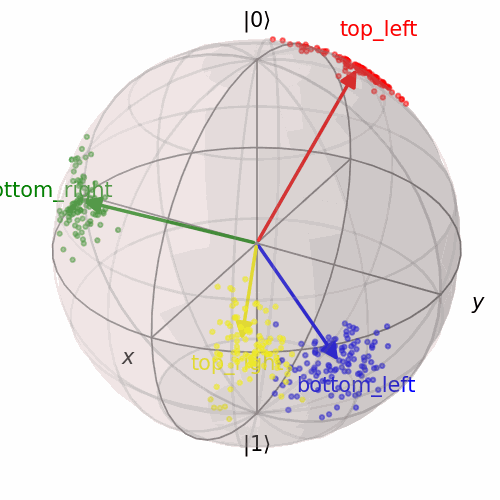
This thesis explores novel approaches to compositional reasoning in AI leveraging the mathematics of quantum theory as a general probabilistic theory. Starting from the quantum picturialism paradigm, offering a diagrammatic category-theoretic language, I show that quantum theory provides practical modelling and computational benefits for AI. A literature survey connect various applications, from quantum game theory and satisfiability to ML, NLP and cognition. How to formally represent and reason with concepts is a longstanding challenge in cognitive science and AI. My thesis studies the Quantum Model of Concepts (QMC), which provides conceptual space theory with quantum theoretical semantics. The diagrammatic language serves as a compositional framework for both, exposing common structures and facilitating insights between domains. I implement the model as a hybrid quantum-classical architecture on real quantum hardware to explore how QMCs can form practical intermediate, compositional representations for artificial agents combining symbolic and subsymbolic reasoning. Addressing the symbol grounding problem, I show that QMC representations can be learned from raw data in a (self-)supervised subsymbolic way, but that composite concepts can also be grounded in simpler ones to be interpretable and data-efficient. By transforming quantum concepts into probabilistic generative processes, the QMC can solve visual relational Blackbird puzzles involving abstraction and perceptual uncertainty, similar to Raven’s Progressive Matrices.
@phdthesis{gauderisQuantumTheoryKnowledge2023, title = {Quantum {{Theory}} in {{Knowledge Representation}}: {{A Novel Approach}} to {{Reasoning}} with a {{Quantum Model}} of {{Concepts}}}, shorttitle = {Quantum {{Theory}} in {{Knowledge Representation}}}, author = {Gauderis, Ward and Wiggins, Geraint}, year = {2023}, month = aug, address = {Brussels, Belgium}, school = {Vrije Universiteit Brussel}, }
Papers
2025
- Finding Manifolds With Bilinear AutoencodersThomas Dooms and Ward GauderisIn Mechanistic Interpretability Workshop: At the Thirty-Ninth Annual Conference on Neural Information Processing Systems, Oct 2025
Sparse autoencoders are a standard tool for uncovering interpretable latent representations in neural networks. Yet, their interpretation depends on the inputs, making their isolated study incomplete. Polynomials offer a solution; they serve as algebraic primitives that can be analysed without reference to input and can describe structures ranging from linear concepts to complicated manifolds. This work uses bilinear autoencoders to efficiently decompose representations into quadratic polynomials. We discuss improvements that induce importance ordering, clustering, and activation sparsity. This is an initial step toward nonlinear yet analysable latents through their algebraic properties.
@inproceedings{dooms_bilinear_2025, title = {Finding Manifolds With Bilinear Autoencoders}, url = {https://openreview.net/forum?id=ybJXIh4vcF}, urldate = {2025-10-13}, booktitle = {Mechanistic Interpretability Workshop: {At} the Thirty-Ninth Annual Conference on Neural Information Processing Systems}, author = {Dooms, Thomas and Gauderis, Ward}, month = oct, year = {2025}, } - Choir in the Loop Singer-Aware AI Composition PracticeFilippo Carnovalini, Ward Gauderis, Joris Grouwels, and 2 more authorsIn Proceedings of the The 6th Conference on AI Music Creativity, Sep 2025
This workshop explores the interaction between AI co-created choral composition and human performance through a live, participatory format: an open rehearsal by Café Latte, the Vrije Universiteit Brussel university choir. Via an open call, we invite contributors to submit SATB pieces curated with choral performability, dynamics and expressivity in mind. Selected works will be rehearsed publicly with the co-creators present, offering a unique opportunity to examine how amateur singers engage with AI-assisted composition. The workshop aims to move beyond evaluation paradigms such as the “Musical Turing Test”, instead encouraging collaborative inquiry into how generative systems can meaningfully interact with vocal practice. By involving composers, performers, and audience members, this session explores the reality of AI music performance and contributes to the development of singer-aware generative models and practices.
@inproceedings{carnovaliniChoirLoopSingerAware2025, title = {Choir in the {{Loop Singer-Aware AI Composition Practice}}}, booktitle = {Proceedings of the {{The}} 6th {{Conference}} on {{AI Music Creativity}}}, author = {Carnovalini, Filippo and Gauderis, Ward and Grouwels, Joris and {Van den Brande}, Margot and Wiggins, Geraint}, year = {2025}, month = sep, publisher = {Zenodo}, address = {Brussels, Belgium}, doi = {10.5281/zenodo.17303733}, urldate = {2025-10-17}, } - Classical Data in Quantum Machine Learning Algorithms: Amplitude Encoding and the Relation Between Entropy and Linguistic AmbiguityJurek Eisinger, Ward Gauderis, Lin Huybrecht, and 1 more authorEntropy, Apr 2025
The Categorical Compositional Distributional (DisCoCat) model has been proven to be very successful in modelling sentence meaning as the interaction of word meanings. Words are modelled as quantum states, interacting guided by grammar. This model of language has been extended to density matrices to account for ambiguity in language. Density matrices describe probability distributions over quantum states, and in this work we relate the mixedness of density matrices to ambiguity in the sentences they represent. The von Neumann entropy and the fidelity are used as measures of this mixedness. Via the process of amplitude encoding, we introduce classical data into quantum machine learning algorithms. First, the findings suggest that in quantum natural language processing, amplitude-encoding data onto a quantum computer can be a useful tool to improve the performance of the quantum machine learning models used. Second, the effect that these encoded data have on the above-introduced relation between entropy and ambiguity is investigated. We conclude that amplitude-encoding classical data in quantum machine learning algorithms makes the relation between the entropy of a density matrix and ambiguity in the sentence modelled by this density matrix much more intuitively interpretable.
- Quantum Methods for Managing Ambiguity in Natural Language ProcessingJurek Eisinger, Ward Gauderis, Lin Huybrecht, and 1 more authorMar 2025
The Categorical Compositional Distributional (DisCoCat) framework models meaning in natural language using the mathematical framework of quantum theory, expressed as formal diagrams. DisCoCat diagrams can be associated with tensor networks and quantum circuits. DisCoCat diagrams have been connected to density matrices in various contexts in Quantum Natural Language Processing (QNLP). Previous use of density matrices in QNLP entails modelling ambiguous words as probability distributions over more basic words (the word }texttt{queen}, e.g., might mean the reigning queen or the chess piece). In this article, we investigate using probability distributions over processes to account for syntactic ambiguity in sentences. The meanings of these sentences are represented by density matrices. We show how to create probability distributions on quantum circuits that represent the meanings of sentences and explain how this approach generalises tasks from the literature. We conduct an experiment to validate the proposed theory.
@misc{eisingerQuantumMethodsManaging2025, title = {Quantum {{Methods}} for {{Managing Ambiguity}} in {{Natural Language Processing}}}, author = {Eisinger, Jurek and Gauderis, Ward and de Huybrecht, Lin and Wiggins, Geraint A.}, year = {2025}, month = mar, number = {arXiv:2504.00040}, eprint = {2504.00040}, primaryclass = {cs}, publisher = {arXiv}, doi = {10.48550/arXiv.2504.00040}, urldate = {2025-10-17}, archiveprefix = {arXiv}, keywords = {Computer Science - Artificial Intelligence,Computer Science - Computation and Language,Quantum Physics}, }
2024
- Compositionality Unlocks Deep Interpretable ModelsIn Connecting Low-Rank Representations in AI: At the 39th Annual AAAI Conference on Artificial Intelligence, Nov 2024
We propose χ-net, an intrinsically interpretable architecture combining the compositional multilinear structure of tensor networks with the expressivity and efficiency of deep neural networks. χ-nets retain equal accuracy compared to their baseline counterparts. Our novel, efficient diagonalisation algorithm, ODT, reveals linear low-rank structure in a multilayer SVHN model. We leverage this toward formal weightbased interpretability and model compression.
@inproceedings{doomsCompositionalityUnlocksDeep24, title = {Compositionality {Unlocks} {Deep} {Interpretable} {Models}}, url = {https://openreview.net/forum?id=bXAt5iZ69l}, urldate = {2025-02-17}, booktitle = {Connecting {Low}-{Rank} {Representations} in {AI}: {At} the 39th {Annual} {AAAI} {Conference} on {Artificial} {Intelligence}}, author = {Dooms, Thomas and Gauderis, Ward and Wiggins, Geraint and Mogrovejo, Jose Antonio Oramas}, month = nov, year = {2024}, }
2023
- Efficient Bayesian Ultra-Q Learning for Multi-Agent GamesWard Gauderis, Fabian Denoodt, Bram Silue, and 2 more authorsIn Proc. of the Adaptive and Learning Agents Workshop (ALA 2023 at AAMAS), May 2023
This paper presents Bayesian Ultra-Q Learning, a variant of Q-Learning adapted for solving multi-agent games with independent learning agents. Bayesian Ultra-Q Learning is an extension of the Bayesian Hyper-Q Learning algorithm proposed by Tesauro that is more efficient for solving adaptive multi-agent games. While Hyper-Q agents merely update the Q-table corresponding to a single state, Ultra-Q leverages the information that similar states most likely result in similar rewards and therefore updates the Q-values of nearby states as well. We assess the performance of our Bayesian Ultra-Q Learning algorithm against three variants of Hyper-Q as defined by Tesauro, and against Infinitesimal Gradient Ascent (IGA) and Policy Hill Climbing (PHC) agents. We do so by evaluating the agents in two normal-form games, namely, the zero-sum game of rock-paper-scissors and a cooperative stochastic hill-climbing game. In rock-paper-scissors, games of Bayesian Ultra-Q agents against IGA agents end in draws where, averaged over time, all players play the Nash equilibrium, meaning no player can exploit another. Against PHC, neither Bayesian Ultra-Q nor Hyper-Q agents are able to win on average, which goes against the findings of Tesauro. In the cooperation game, Bayesian Ultra-Q converges in the direction of an optimal joint strategy and vastly outperforms all other algorithms including Hyper-Q, which are unsuccessful in finding a strong equilibrium due to relative overgeneralisation.
@inproceedings{gauderisEfficientBayesianUltraQ2023, title = {Efficient {{Bayesian Ultra-Q Learning}} for {{Multi-Agent Games}}}, url = {https://alaworkshop2023.github.io/papers/ALA2023_paper_57.pdf}, urldate = {2024-11-23}, booktitle = {Proc. of the {{Adaptive}} and {{Learning Agents Workshop}} ({{ALA}} 2023 at {{AAMAS}})}, author = {Gauderis, Ward and Denoodt, Fabian and Silue, Bram and Vanvolsem, Pierre and Rosseau, Andries}, year = {2023}, month = may, }
Other
2024
- Quantum Theory in Knowledge Representation: A Novel Approach to Reasoning with a Quantum Model of ConceptsWard Gauderis and Geraint WigginsIn Pre-Proceedings of BNAIC/BeNeLearn 2024, Nov 2024
@inproceedings{bnaic, title = {Quantum {{Theory}} in {{Knowledge Representation}}: {{A Novel Approach}} to {{Reasoning}} with a {{Quantum Model}} of {{Concepts}}}, shorttitle = {Quantum {{Theory}} in {{Knowledge Representation}}}, booktitle = {Pre-Proceedings of {{BNAIC}}/{{BeNeLearn}} 2024}, year = {2024}, month = nov, address = {Utrecht}, author = {Gauderis, Ward and Wiggins, Geraint}, url = {https://bnaic2024.sites.uu.nl/wp-content/uploads/sites/986/2024/11/Quantum-Theory-in-Knowledge-Representation-A-Novel-Approach-to-Reasoning-with-a-Quantum-Model-of-Concepts.pdf}, } - Quantum Theory in Knowledge RepresentationWard GauderisBrEA Magazine, Jan 2024
@article{brea, title = {Quantum {{Theory}} in {{Knowledge Representation}}}, author = {Gauderis, Ward}, year = {2024}, month = jan, journal = {BrEA Magazine}, volume = {4}, number = {1}, pages = {14--16}, url = {https://www.brea.be/magazines/brea-magazine-januari-maart-2024}, } - Compositional Tensor Neural NetworksWard Gauderis and Thomas DoomsIn iDEPOT 146658, Aug 2024
@inproceedings{gauderisCompositionalTensorNeural2024, title = {Compositional {{Tensor Neural Networks}}}, booktitle = {{{iDEPOT}} 146658}, author = {Gauderis, Ward and Dooms, Thomas}, year = {2024}, month = aug, publisher = {Benelux Office for Intellectual Property}, }
2023
- Blackbird DatasetWard GauderisAug 2023
A dataset of synthetic relational puzzles, inspired by the RAVEN dataset.
@misc{gauderisWardGauderisBlackbird2023, title = {{{Blackbird Dataset}}}, author = {Gauderis, Ward}, year = {2023}, month = aug, urldate = {2025-09-15}, publisher = {GitHub}, howpublished = {\url{https://github.com/WardGauderis/Blackbird}}, url = {https://github.com/WardGauderis/Blackbird}, }